无限猴子定理,让猴子一直按键盘可以打出莎士比亚的全套著作？

【知识】

无限猴子定理是什么了？无限猴子定理的大概意思是，如果让一只猴子在打字机上随机地进行按键，如果一直不停的这样按下去，只要时间达到无穷时，这只猴子就几乎必然可以打出任何给定的文字，甚至是莎士比亚的全套著作也可以打出来。
这说得实在是太夸张了，猴子虽然是一只比较聪明的动物，但是让他打字，别说是莎士比亚的全套著作了，就算是简单的几句话，也很以出来吧，就算是人，让你打出莎士比亚的全套著作估计也无法办到，那么无限猴子定理到底是什么样的定理了，下面就来了解一下吧。

无限猴子定理的起源
无限猴子定理最早是由埃米尔·博雷尔在1909年出版的一本谈概率的书籍中提到的，此书中介绍了“打字的猴子”的概念。无限猴子定理是概率论中的柯尔莫哥洛夫的零一律的其中一个命题的例子。不过，当波莱尔在书中提出零一律的这个特例时，柯尔莫哥洛夫的一般叙述并未给出（柯尔莫哥洛夫那本概率论的著作直到1933年才出版）。
但是要说到无限猴子定理的典故最早的出处，却是在1792年的，乔纳森·斯威夫特出版的的《格列佛游记》，在《格列佛游记》的第三部分第五章中，教授要求学生通过经常转动机械把手产生一些随机的字句，以建立所有科学知识的列表。
无限猴子定理的理论变化十分的多，可以包括多个甚至无限个打字员，目标文本也可以从一个简单的句子到完整的图书馆的书，而这些有关概率的说法，最最可以追述到亚里士多德所写的《论产生和毁灭》和西塞罗的所写的《论神之本性》，后来这些表述经过了布莱兹·帕斯卡和乔纳森·斯威夫特最后以形象的打字员的形式表示了出来。
在20世纪早期，埃米尔·博雷尔和亚瑟·爱丁顿运用这个理论在统计力学基础中阐述隐式时间标尺。

无限猴子定理的直接证明
两个独立事件同时发生的概率等于其中每个事件单独发生的概率的乘积。比如，在某一天悉尼下雨的可能性为0.3，旧金山地震的可能性是0.008（这两个事件可以视为相互独立的），那么它们同时发生的概率是0.3×0.008 = 0.0024。
假设一个打字机有50个键，想要打出的字是“banana”。随机的打字时，打出第一个字母“b”的概率是1/50，打出第二个字母“a”的概率也是1/50，因为事件是独立的，所以一开始就打出单词“banana”的概率是：

(1/50)×(1/50)×(1/50)×(1/50)×(1/50)×(1/50) =(1/50)6，
这个概率小于150亿分之1。同理，接下来继续打出“banana”的概率也是1/506。

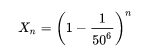
随着n变大，Xn在变小。当n等于100万时，Xn大约是0.9999（没有打出“banana”的概率是99.99%）；但是当n等于100亿时Xn大约是0.53（没有打出“banana”的概率是53%）；当n等于1000亿时Xn大约是0.0017（没有打出“banana”概率是0.17%）;当n趋于无穷时Xn趋于零。这就是说，只要使n足够大，Xn可以变得足够小。

同样的论证也可以说明在无限多的猴子中有至少一个会打出一段特定的文章。这里Xn =(1−(1/50)6)n，其中Xn表示在前n个猴子中没有一个一次打出banana的概率。当我们有1000亿只猴子时，这个概率降低到0.17%，并且随着猴子数量n趋于无穷大，没有打出“banana”的概率Xn趋于0。

但是，在只有有限的时间和有限只猴子时，结论就大不一样了。如果我们的猴子数量和可观测宇宙中的基本粒子数量一样多，大约1080只，每秒钟打1000个字，持续打100倍于宇宙的生命长度的时间（大约1020秒）有猴子能够打出一本很薄的书的概率也趋近于0。

无限猴子定理中的猴子真的能打出哈姆雷特这本书吗

这当然是不可能的，现实中，猴子打出一篇像样的文章的概率是零，因为科学家经过反复试验后发现，猴子（或猩猩）在使用键盘时通常会连按某一个键或拍击键盘，2003年，普利茅斯大学艺术媒体实验室课程的教师和学生使用2,000英镑津贴做了这个实验，结果打出了5张全是‘S’的纸。最终打出的文字不可能成为一个完整的句子。[8]这是因为现实是非常大的有限，而不是严格意义上的无限。

标签：数学